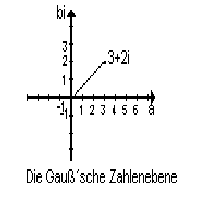
| HOME | NEWS | AWARDS | ABOUT ME | TEXTE | REFERATE | PROJEKTE |
| MUSIK | CHAT | SPECIAL | LINKS |
Gleich zum 2. Teil (Rechnen mit komplexen Zahlen)
Beim Zahlenbereich der komplexen Zahlen handelt es sich um eine Erweiterung der reelen Zahlen. Im folgenden wird kurz der Grund der Einführung dieses Zahlenbereichen dargelegt werden. Zuerst hatte man nur die ganzen Zahlen zum Rechnen. Diese Zahlen können auch als Punkte auf dem Zahlenstrahl dargestellt werden. Nun ist es aber auch möglich Dinge zu teilen, so dass einzelne Stücke lediglich Teile des Ganzen sind. Diese Erkenntnis führte zur Einführung der gebrochenen Zahlen (im Rahmen der weiter unten beschriebenen Komplexen Zahlen kommt es dann sogar zu gebrochenen Dimensionen). Eine gebrochene Zahl besteht stets aus einem Zähler und einem Nenner, wobei der Nenner angibt, in wieviele Teile ein Ganzes zerlegt wird und der Zähler, wieviele dieser Teile vorhanden sind. Dieser Zahlenbereich umfasst auch den Bereich der ganzen Zahlen, wobei hier der Zähler stets ein Vielfaches des Nenners ist. Gebrochene Zahlen sind auf dem Zahlenstrahl zwischen den ganzen Zahlen anzusiedeln und verbinden die Punkte der ganzen Zahlen zu einer scheinbaren Linie. Ein weiteres Problem tauchte auf, als man versuchte eine grössere Zahl von einer kleineren abzuziehen. Das war bis dato unmöglich, da der Zahlenstrahl nach einer Seite bei Null begrenzt war. Um das Problem zu lösen, führte man die rationalen Zahlen ein, welche wiederum die gebrochenen und damit auch die ganzen Zahlen beinhalten. Als Erweiterung wurde der Zahlenstrahl an der Null gespiegelt. Um die Zahlen links der Null von denen rechts der Null unterscheiden zu können, hat man allen Zahlen links von der Null ein Minus vorgesetzt. Die negativen Zahlen waren geschaffen. Der Zahlenstrahl war nun nach beiden Seiten unbegrenzt, aber war er auch wirklich schon ein Strahl, an dem jeder Zahl ein Punkt und umgekehrt zugewiesen werden konnte? Dieses Problem tauchte auf, als man beispielsweise versuchte eine Zahl zu finden, welche quadriert 2 ergibt. Man stellte fest, dass man zwar durch Näherung sich beliebig nahe an die 2 nähern kann, jedoch keine exakte Zahl zu finden ist. Auch stellte man fest, dass man unendlich viele Nachkommastellen jener Zahl berechnen kann und niemals eine Periodizität eintritt, was bedeutet, dass sich die Zahl nicht als Bruch darstellen lässt. Diesen Zahlen, welche sich nicht als Bruch schreiben lassen, gab man den Namen irrationale Zahlen. Zusammen ergeben die rationalen und irrationalen Zahlen den Bereich der reellen Zahlen und bilden den aus dem Unterricht bekannten Zahlenstrahl. Obwohl man nun einen lückenlosen Zahlenstrahl hat gibt es immernoch Zahlen, welche sich nicht auf ihm darstellen lassen, wie z.B. die Wurzel aus minus eins. Andersherum formuliert heisst das Problem: Welche Zahl ergibt ins Quadrat genommen minus eins. Keine der bekannten Zahlen erfüllte diese Bedingung, weshalb ein neuer Zahlenbereich geschaffen werden musste: die komplexen Zahlen. In den komplexen Zahlen führte man die imaginäre Einheit "i" ein. Imaginär deshalb, weil man damals dachte, dass alle Zahlen auf dem Zahlenstrahl von Gott geschaffen, also real seien. Die komplexen Zahlen hingegen sind Schaffung des menschlichen Vorstellungsvermögens, sprich imaginär. Heute weiss man, dass alle Zahlen eigentlich nur in unserer Vorstellung existieren, also imaginär sind. Man definierte, dass "i" im Quadrat gleich minus eins ist.
Merke: i*i = -1
Wie aber sollte man die komplexen Zahlen darstellen? Der Zahlenstrahl bot keinen Platz mehr für neue Zahlen, also erweiterte man den Strahl den man als X-Achse (reelle Achse) betrachten kann um eine Y-Achse (imaginäre Achse), auf der Vielfache von "i" abgetragen werden. Das damit enstandene Gebilde nennt sich Gauss'sche Zahlenebene.
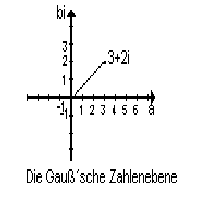
Da in einer Ebene jeder Punkt mit zwei Koordinaten bezeichnet werden kann, gilt dies folglich auch für die komplexen Zahlen. Die X-Koordinate enstpricht dabei dem reellen Anteil einer Zahl, die Y-Koordinate dem imaginären, als Vielfaches von "i". Daraus folgt, dass sich eine komplexe Zahl z wiefolgt schreiben lässt:
z = a + b*i (a=reeller Anteil; b=imaginärer Anteil).
Das Plus zwischen a und b*i kommt daher, dass jeder reellen Zahl im Bereich der komplexen Zahlen noch ein imaginärer Teil hinzugefügt wird (wie auch schon bei den gebrochenen Zahlen, wo einer ganzen Zahl noch ein gebrochener Teil hinzugefügt wird, z.B. 3/2=1+1/2). Ein Punkt in der Ebene lässt sich aber auch mit Hilfe der Sätze für das rechtwinklige Dreieck darstellen. Dazu ist es jedoch notwendig die Länge der Hypothenuse zu kennen. Diese ergibt sich nach Pythagoras aus der Wurzel des Quadrates der beiden Katheten, also a und b. Bei den komplexen Zahlen heisst die Hypothenuse Betrag der Zahl. Der Betrag |z| ergibt sich wiefolgt:
|z| = sqrt(a*a + b*b) (sqrt=squareroot=Quadratwurzel).
Daraus folgt die Schreibweise in Polarkoordinaten:
a = |z|*cos c (c=Winkel zwischen reeller Achse und Betrag)
b*i= i*|z|*sin c
z = |z|*(cos c + i*sin c)
Die Einführung der komplexen Zahlen schuf auch ganz neue Themengebiete, wie die Fraktale.
Rechnen mit komplexen Zahlen (Zurück zum Anfang)
Die komplexen Zahlen beinhalten auch die reellen Zahlen, wobei hier der imaginäre Teil Null ist. Die zweite Schreibweise in Polarkoordinaten erhält ihren Sinn, wenn man versucht komplexe Zahlen zu multiplizieren oder zu dividieren. Für die Addition und Subtraktion ist jedoch die erste Schreibweise zu empfehlen. Für diese beiden Rechenarten gestaltet sich auch das Rechnen entsprechend einfach.
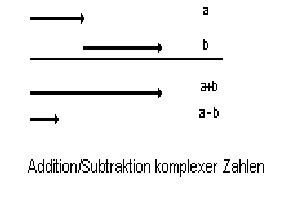
z1+z2 = (a1+b1*i)+(a2+b2*i) = (a1+a2)+(b1+b2)*i
z1-z2 = (a1+b1*i)-(a2+b2*i) = (a1-a2)+(b1-b2)*i
Auf dem Zahlenstrahl lässt sich dies wiefolgt erklären: Der reelle Anteil einer Zahl ist eine Strecke auf der reellen Achse, die vom Punkt Null bis zum entsprechenden Wert der reellen Zahl geht. Addiert man nun einen zweiten Wert hinzu, so ist das Ergebnis die Länge beider Strecken zusammengenommen. Gleiches lässt sich auch auf der imaginären Achse darstellen. Bei der Subtraktion ist das Ergebnis gleich der Differenz beider Strecken.
Nimmt man die Schreibweise z=a+b*i für eine komplexe Zahl, so ist die Multiplikation ein reines Ausmultiplizieren. Diese Vermutung ist berechtigt, da die komplexen Zahlen eine Erweiterung der reellen Zahlen darstellen und möglichst auch deren Gesetze zum Rechnen übernehmen sollten, so auch das Distributivgesetz ( a*(b+c)=a*b+a*c ).
z1*z2 = (a1+b1*i)*(a2+b2*i)
= a1*a2 + a1*b2*i + a2*b1*i + b1*b2*i*i
da i*i=-1,
z1*z2 = (a1*a2-b1*b2) + (a1*b2+a2*b1)*i
Die Division in dieser Schreibweise gestaltet sich etwas schwieriger, da hier sowohl im Zähler, als auch im Nenner komplexe Zahlen stehen. Um dividieren zu können, muss man den Bruch so erweitern, dass im Nenner eine reelle Zahl steht. Dazu benutzt man die 3. Binomische Formel die bei komplexen Zahlen wiefolgt aussieht:
(a+bi)*(a-bi) = a*a-b*b*i*i = a*a-b*b*(-1)
= a*a+b*b .
Die Zahl z2, die zu z1 bis auf das Vorzeichen des imaginären Teils identisch ist heisst konjugiert zu z1, d.h. a-b*i ist die konjugierte Zahl zu a+b*i. Daraus folgt, dass man zum Dividieren den Bruch mit der zum Nenner konjugierten Zahl erweitern muss.
(a1+b1*i) (a1+b1*i)*(a2-b2*i)
---------- = --------------------
(a2+b2*i) a2*a2+b2*b2
(a1*a2+b1*b2) (a1*b2+a2*b1)*i
= ------------- + ---------------
a2*a2+b2*b2 a2*a2+b2*b2
Wie oben schon erwähnt gestalten sich Multiplikation und Division einfacher in der Polarform. Auch hier wird ersteinmal ausmultipliziert:
z1*z1 = |z1|*(cos c1 +i*sin c1)*|z2|*(cos c2 +i*sin c2)
= |z1|*|z2|*(cos c1 *cos c2 +i*i*sin c1 *sin c2 +
i*(cos c1 *sin c2 + cos c2 *sin c1)
Zusammengefasst nach den Additionstheoremen:
z1*z2 = |z1|*|z2|*[ cos(c1+c2)+i*sin(c1+c2) ]
Das heisst, die Multiplikation zweier komplexer Zahlen bedeutet die Multiplikation ihrer Beträge und die Addition ihrer Winkel. Da die Division zur Multiplikation invers ist, sind bei der Division in Polarkoordinaten die Beträge zu dividieren und die Winkel voneinander abzuziehen:
z1 |z1|
-- = ---- * [ cos(c1-c2)+i*sin(c1-c2) ] .
z2 |z2|
Aus der Rechenvorschrift für die Multiplikation in Polarkoordinaten lässt sich leicht die Rechenvorschrift für das Potenzieren von komplexen Zahlen herleiten, da es sich lediglich um eine mehrfache Malnehmen einer Zahl mit sich selber handelt. Bei der Multiplikation werden die Beträge miteinander multipliziert. Daraus folgt, dass beim Quadrieren einer komplexen Zahl der Betrag mit sich selber multpliziert werden muss, er wird quadriert. Beim Rechnen mit der Potenz 3 wird das Ergebnis vom Quadrieren noch einmal mit der Ausgangszahl multipiziert, d.h. das Quadrat des Betrages wird mal den Betrag genommen und man erhält den Betrag hoch 3. Allgemein ist also festzuhalten, dass beim Potenzieren einer komplexen Zahl mit dem Exponenten n, der Betrag der Zahl hoch n genommen wird. Nun müssen bloss noch die Argumente der Sinus- und Kosinusfunktion in Polarkoordinaten bestimmt werden. Bei der Multiplikation werden die Winkel beider komplexen Zahlen addiert. Gleiches passiert auch beim Potenzieren, mit dem Unterschied, dass die Winkel gleich sind, d.h. beim Quadrieren einer komplexen Zahl mit dem Winkel c erhält man als Argument der Sinus- und Kosinusfunktion c+c=2*c. Beim Rechnen mit der Potenz 3 wird diesem Argument noch einmal der Winkel c hinzuaddiert und es ergibt sich als Argument 3*c. Allgemein formuliert: Das Argument der Sinus- und Kosinusfunktion einer komplexen Zahl in Polarkoordinaten beim Potenzieren mit dem Exponenten n ist n mal den Winkel der komplexen Zahl.
z^n = |z|^n*[ cos(n*c)+i*sin(n*c) ]
Das Radizieren (Wurzelziehen) ist ebenfalls mit dieser Formel möglich, da es sich lediglich um eine Potenzierung um den Wert 1/n handelt, wobei n gleich dem Grad der Wurzel ist. Nur ist hierbei die Periodizität der Sinus- und Kosinusfunktion zu beachten. Der Sinus des Winkel c ist gleich dem Sinus von c+360 Grad oder c+720 Grad (gleiches gilt für den Kosinus). Diese Beziehung führt dazu, dass die n-te Wurzel im Bereich der komplexen Zahlen genau n Lösungen hat. Dazu muss man c genau (n-1)-Mal um 360 Grad erhöhen und jeweils die Lösung berechnen. Wenn man n-Mal 360 Grad addiert erhält man wieder den Wert den man beim Einsetzen von c erhalten würde.
z^(1/n) = |z|^(1/n)*
[ cos((1/n)*(k*360+c))+i*sin((1/n)*(k*360+c)) ]
(für k e N; k=(0;1;..;n-1))
Diese Gleichung wird auch Kreisteilungsgleichung genannt, da ihre Lösungen einen Kreis in genau n gleiche Teile zerteilen. In der Normalform a+b*i geschieht das Quadrieren nach den Binomischen Formeln:
z^2 = (a+b*i)^2 = a^2+b^2*i^2+2*a*b*i = a^2-b^2+2*a*b*i
Das Radizieren in der Normalform ist nicht sinnvoll, da es leichter ist, die komplexe Zahl in Polarkoordinaten zu bringen und die einheitliche Rechenvorschrift anzuwenden. Gleiches gilt auch für das Potenzieren mit grossen Exponenten.
Eine tolle Anwendung von komplexen Zahlen ist die Erstellung von Fraktalen, welche u.a. durch die Forschungen von Benoit Mandelbrot bekannt wurden.
Zurück zum Anfang des Dokuments, oder nocheinmal zum 2. Teil.
Autor : Jens Koopmann Letzte änderung: 07.01.96
| HOME | NEWS | AWARDS | ABOUT ME | TEXTE | REFERATE | PROJEKTE |
| MUSIK | CHAT | SPECIAL | LINKS |