| HOME | NEWS | AWARDS | ABOUT ME | TEXTE | REFERATE | PROJEKTE |
| MUSIK
| CHAT
| SPECIAL | LINKS |
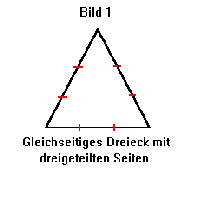
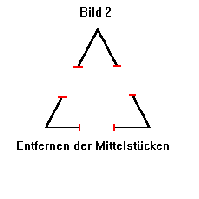
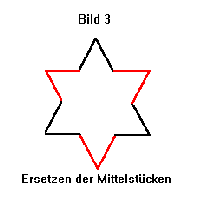
Mandelbrot wurde einmal gefragt, wie genau das Ergebnis einer Messung sein würde, wenn man die Länge der Küste Großbritanniens von einem Flugzeug aus messen würde. Mandelbrot antwortete, daß das Ergebnis wahrscheinlich in keinster Weise der Realität entsprechen würde. Er hatte recht mit dieser Behauptung. Durch die Höhe des Flugzeuges würden kleine Buchten bei der Messung verloren gehen. Aber selbst wenn man die Küste ablaufen würde und immer gerade Stäbe mit einem halben Meter Länge aneinander legen würde, wäre das Ergebnis nur unwesentlich genauer. Selbst wenn man jedes Sandkorn vermessen würde, wäre das Ergebnis falsch, da es immer noch Einschnitte geben würde, die teilweise nicht einmal sichtbar sind und somit nicht berücksichtigt werden. Der Schluß, der sich daraus ziehen läßt, ist, daß die Küste von Großbritannien unendlich lang ist. Die Fläche des Landes ist jedoch trotzdem begrenzt. Wie kann es also kommen, daß ein Gebilde einen unendlich großen Umfang hat, jedoch eine endlich große Fläche besitzt. Ein Modell für die Küste lieferte dabei der Wissenschaftler Koch mit seiner optimalen Schneeflocke. Dabei wird jede Seite eines gleichseitigen Dreieckes in drei Teile zerlegt. Das Mittelteil jeder Seite wird herausgenommen und durch 2 Teile gleicher Länge ersetzt (siehe Bild1-3).



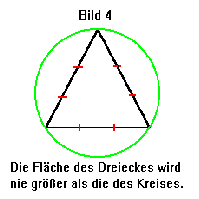
Jede der Seiten hat nun 4/3 ihrer ursprünglichen Länge, folglich auch der Umfang. Entstanden ist dabei ein Stern mit dessen Seiten das Verfahren wiederholt wird. Mit der Ergebnisfigur ebenfalls u.s.w. Dadurch, daß der Umfang mit jedem Schritt auf 4/3 des vorhergehenden Wertes ansteigt, wird er gegen Unendlich streben. Die Fläche des Dreiecks läßt sich jedoch begrenzen, indem man einen Kreis um das Ursprungsdreieck zieht, der die Eckpunkte des Dreieckes berührt. Der Mittelpunkt des Kreises liegt in der Mitte des Dreieckes (siehe Bild 4).
Ein anderes Gebilde ist das Sierpinskidreieck(Bild 5), wo ein gleichseitiges Dreieck in vier kleine gleichseitige Dreiecke zerlegt wird, wobei das Mittlere entnommen wird. Der Umfang des Dreiecks wird dadurch größer, seine Fläche jedoch kleiner. Gleiches kann man dann mit den verbleibenden 3 Dreiecken machen und wird nach mehrmaliger Fortführung dieses Vorgangs feststellen, daß die Fläche des Gebildes gegen Null strebt während der Umfang gegen unendlich strebt.
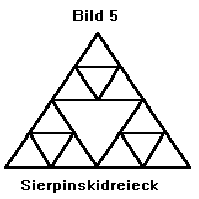
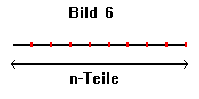
Diese Eigenschaften einen unendlich großen Umfang zu haben und dabei keine oder eine beschränkte Fläche zu haben, erfüllen keine unserer ein-, zwei- oder dreidimensionalen Gebilde (bei 3D-Gebilden ist der Umfang gleich der Kantenlänge und die Fläche das Volumen). Deshalb bedient man sich zunächst einer anderen Darstellung der Dimension. Nimmt man eine Strecke (Bild 6) und teilt diese in n gleichgroße Teile, so enstpricht die Länge der einzelnen Stücke gleich 1/n des Gesamten. Das Verhältnis zwischen Gesamtstrecke und Teilstrecke ist also 1:n. Das n in diesem Verhältnis wird im folgenden mit r bezeichnet.
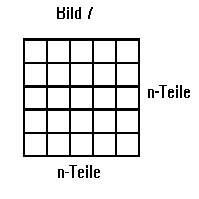
Das gleiche Verfahren wendet man nun auf ein Rechteck an, welches im Gegensatz zur Strecke zweidimensional ist (Bild 7). Auch hier werden die Seiten in n gleiche Teile zerlegt. Dabei entstehen n*n kleine Rechtecke deren Seitenlänge gleich 1/n im Vergleich zum Gesamten ist. r ist also auch hier wieder n.
Um von n*n wieder auf n zu kommen muß also die Quadratwurzel gezogen werden. Bei der Strecke muß aus n ebenfalls n gemacht werden, was der 1. Wurzel von n entspricht. Es läßt sich daher folgende Gleichung aufstellen:
r=D-te Wurzel(n) (D entspricht der Dimension)
Bei der Strecke verhält sich das wiefolgt: r=1.Wurzel(n)=n, was in der Tat stimmt. Gleiches müßte ebenfalls beim Rechteck herauskommen: r=2.Wurzel(n*n) =n, wie erwartet. Man hat also eine Gleichung gefunden, die man nun nach D, also der Dimension umstellt:
lg n
D=log r(n)=------- (log r(n)=Logarithmus von
lg r n zur Basis r)
Diese Gleichung wendet man nun auf die Kochkurve an. Dabei ist die Anzahl der Teilstücke, die aus einem entstehen stets 4, also gilt: n=4. Das Verhältnis der Teilstücke zum Gesamten ist hier jedoch nicht n, wie es bei dem Rechteck und der Strecke der Fall war, sondern 1:3. Deshalb gilt: r=3. Als nächstes setzt man in die Gleichung ein und löst sie:
lg 4
D= ------ = 1,2618
lg 3
Es ergibt sich eine Dimension von 1,26 für die Kochkurve. Gleiches für das Sierpinskidreieck:
n=3 (Anzahl der verbleibenden Teilflächen nach dem
Herausnehmen des Mitteldreieckes)
r=2 (Länge der Dreickecksseiten ist halb solang wie
die des Gesamten)
lg 3
D= ------ = 1,585
lg 2
Auch hier ergibt sich also eine gebrochene Dimension, was es ja zu zeigen galt.
| HOME | NEWS | AWARDS | ABOUT ME | TEXTE | REFERATE | PROJEKTE |
| MUSIK
| CHAT
| SPECIAL | LINKS |